Paradoks Zeno yang Tak Terselesaikan Selama Ribuan Tahun

Quote:Monggo di dan timpuk ane

Bila banyak orang ingin menyelesaikan masalah maka berbeda dengan para filosof. Para filosof justru mencari-cari masalah. Sesuatu yang biasa-biasa saja bisa menjadi masalah serius bila ditangani filosof.

Bagaimana dengan jago matematika? Mirip juga dengan para filosof, suka mencari-cari masalah. Sebenarnya mereka â€" filosof atau jago matematika â€" mencari masalah untuk kemudian diselesaikan. Hanya saja sering terjadi adalah masalahnya ketemu tetapi penyelesaiannya tidak ditemukan sampai ribuan tahun kemudian.



Ada salah satu masalah yang ratusan tahun tak terselesaikan, yaitu “Paradoks Zeno.”

Quote:Paradoks Zeno



Achilles dan kura-kura akan berlomba lari 100 meter. Achilles dapat berlari dengan kecepatan 10 meter per detik, sedangkan kura-kura hanya mampu berlari 1 meter per detik.

Well, dari head-to-head kecepatan itu, Achilles â€"selain manusia perkasa juga sportif â€" berbaik hati memberikan keuntungan start bagi sang kura-kura 10 meter di depannya. Tidak masalah, mungkin begitu pikir Achilles. Jadi, siapa yang menang?

Okay. Kura-kura memulai start 10 meter di depan Achilles. Keduanya lalu mulai berlari.

- Setelah satu detik, Achilles telah mencapai tempat di mana kura-kura memulai start-nya. Sedangkan sang kura-kura sudah berlari 1 meter di depan.
- Achilles berlari lagi dan berhasil mencapai tempat kura-kura berada tadi. Sedangkan sang kura-kura telah berlari 0.1 meter di depan.
- Achilles masih dengan semangat berlari lagi untuk meraih selisih 0.1 meter ini. Di saat yang bersamaan, sang kura-kura telah berlari 0.01 meter di depan.

Hal ini berlangsung terus-menerus. Setiap kali Achilles berhasil mencapai tempat di mana kura-kura berada beberapa saat yang lalu, sang kura-kura lagi-lagi telah menempuh sedikit jarak … dan tetap berada di depan Achilles.



Betapapun kerasnya Achilles berusaha, Achilles hanya mampu memperkecil jarak sepersepuluh dari sebelumnya. Ya.. Achilles tidak akan pernah bisa menyusul kura-kura.

Perlombaan ini mungkin tidak selesai dalam waktu yang ditentukan. Kalaupun penonton bosan dan minta lomba dihentikan, kura-kura tetap berada di depan Achilles. Ini yang membuat Achilles frustrasi dan merasa tidak senang, mungkin dia juga menyesal kenapa membiarkan kura-kura memulai lomba 10 meter di depannya. Penyesalan memang datang belakangan.



Argumen zeno ini secara logika tampaknya benar, tapi tidak sesuai dengan kenyataan. Di dunia nyata, Achilles tentu saja menang dengan mudah. Lantas, kenapa logika menunjukkan Achilles tidak mampu menyusul kura-kura?

Ketika orang mendengar paradoks Zeno maka mereka pasti bangkit melawan. Ada 2 golongan orang yang menentang Zeno ini. Golongan pertama mengatakan bahwa paradoks Zeno itu tidak sesuai dengan realitas dan salah. Selesai urusan.

Golongan kedua juga menyatakan paradoks Zeno itu salah. Tapi mereka tidak puas dengan jawaban sederhana sekedar menghakimi salah. Golongan kedua inilah yang lebih dari dua ribu tahun belum puas merumuskan solusi untuk Zeno. Hasil sampingan dari solusi ini adalah berkembangnya ilmu pengetahuan.

Jadi, bagaimana menjawab Paradoks Zeno tersebut?

Spoiler for Jawaban dari Paradoks ZenoSpoiler for Yakin gak dipikirin dulu gan?Spoiler for Oke ini jawaban2 nya
Spoiler for Solusi 1: dengan mempertimbangkan finish
Solusi dengan Mempertimbangkan Finish

Pada jamannya, Zeno memiliki banyak kesulitan tentang notasi angka dan simbol matematika. Saat itu nyaris hanya tersedia bahasa saja. Sedangkan saat ini kita memiliki notasi matematika yang sangat memudahkan. Kita akan memanfaatkan notas persamaan aljabar sederhana untuk menyelesaikan paradoks Zeno ini.

Finish 10 meter
Jelas kura-kuralangsung menang. Bahkan sebelum mereka bergerak kura-kura sudah mencapai finish. Tidak ada masalah pada kasus ini.

Finish 11 meter
Kura-kurajuga menang mencapai finish duluan dalam waktu 1 detik. Sedangkan Achilles baru menempuh jarak 10 meter, masih di belakang kura-kura.

Finish 12 meter
Kali ini kura-kura kalah. Achilles memenangkan pertandingan. Untuk mencapai finish 12 meter, kura-kura perlu waktu 2 detik.
10 m + 2 detik x 1 meter/detik = 12 meter.
Sedangkan Achilles dalam 2 detik, Achilles sudah menempuh jarak 20 meter. Jadi, Achilles sudah menyalip kura-kura beberapa saat sebelumnya.

Finish lebih dari 12 meter
Jelas Achilles akan terus memenangkan untuk finish yang lebih jauh dari 12 meter. Semua sepakat dengan ini.



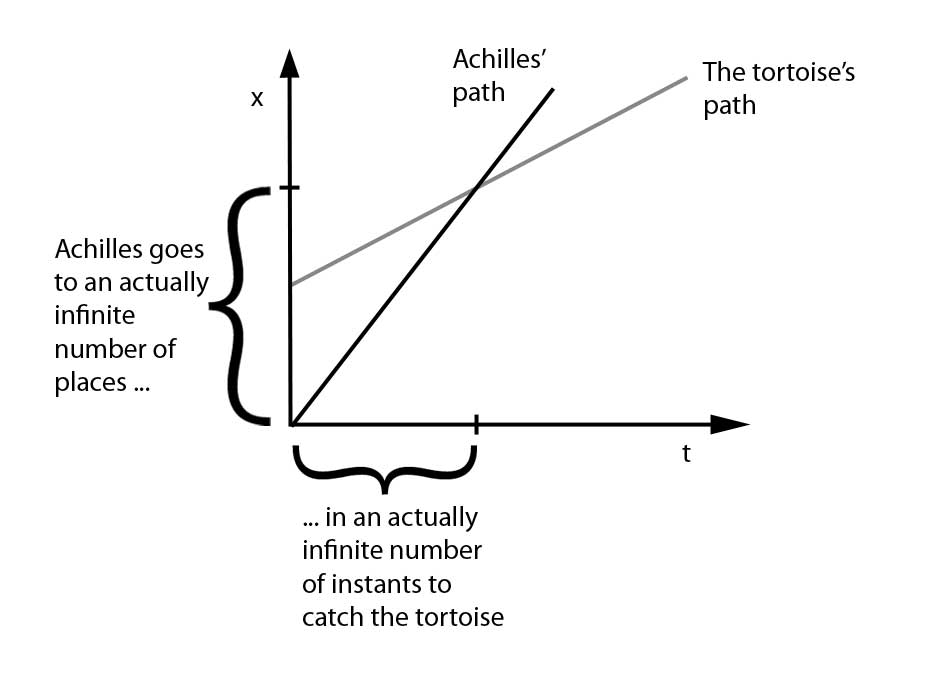
Zeno sekarang mengajukan pertanyaan,
“Bagaimana proses terjadinya Achilles menyalip kura-kura?”

Pertanyaan yang bagus. Begini jawabannya.

Jarak tempuh Achilles = jarak tempuh kura-kura
10.t = 10 + 1.t
9.t = 10
t = 10/9 (detik)

Jadi pada saat waktu t = 10/9 detik Achilles berhasil menyusul kura-kura.

Jarak tempuh Achilles = 10 x 10/9 = 100/9 meter = 11,111 meter.
Jarak tempuh kura-kura = 10 + 1.10/9 = 100/9 meter = 11,111 meter.

Tetapi Zeno masih keberatan dengan penjelasan tersebut.
Spoiler for Solusi 2: dengan teori Himpunan
Solusi Paradoks Zeno dengan Teori Himpunan



Kekuatan teori himpunan dalam matematika sudah tidak diragukan lagi. Lebih dari itu, teori himpunan juga dapat membantu kita memecahkan masalah sehari-hari. Kali ini kita selesaikan paradoks Zeno dengan meminjam teori himpunan.

Mari kita bagi kondisi balapan ini menjadi 3 himpunan berdasar waktu.
A = { kondisi balapan dari waktu t = 0 sampai t kurang 10/9 detik }
B = { kondisi balapan ketika tepat waktu t = 10/9 detik }
C = { kondisi balapan ketika waktu lebih dari 10/9 detik }

Dengan hitungan aljabar sederhana kita dapat menentukan selisih jarak yang ditempuh kura-kura dan Achilles.

jarak kura-kura â€" jarak Achilles = s = (10 + 1.t) â€" (10t)
s = 10 â€" 9t

Perhatikan bahwa masing-masing kondisi akan menunjukan situasi yang berbeda.
A = { 0 < t < 10/9 maka s > 0 maka kura-kura menang }
B = { t = 10/9 maka s = 0 maka kura-kura tepat sama dengan Achilles }
C = { t > 10/9 maka s < 0 maka kura-kura kalah }

Jadi kita memiliki tiga himpunan A, B, dan C yang saling berbeda. Dari sini kita bisa paham penjelasan dari Zeno bahwa kura-kura memenangkan pertandingan. Dan penjelasan Zeno ini benar tanpa ada salah sama sekali. Selesai sudah tanpa ada paradoks.

Bahwa Zeno mengatakan setiap Achilles mendekati kura-kura maka kura-kura telah melangkah sedikit ke depan, itu selalu benar pada situasi himpunan A. Sedangkan intuisi kita mengatakan bahwa Achilles pada akhirnya akan menang. Intuisi umum kita sah pada kondisi himpunan C. Karena dua kondisi di atas â€" kondisi himpunan A dan himpunan C â€" sama-sama sah tetapi keduanya bertentangan maka terjadilah paradoks Zeno ini.

Seandainya kondisi A tidak sah maka kita dengan mudah mengatakan bahwa Zeno salah dan yang benar adalah intuisi sekilas, kondisi C.

Pertanyaan selanjutnya, adakah himpunan A yang sekaligus himpunan C?
Atau apakah irisan himpunan A dan himpunan C?
Atau apakah mungkin kura-kura menang dan sekaligus kura-kura tidak menang?

Jawabannya adalah himpunan kosong = {}.

Jadi jelas, bahwa penyebab paradoks Zeno adalah menganggap ada “suatu kejadian” pada himpunan kosong. Sedangkan yang benar, pada himpunan kosong adalah benar-benar kosong.

Jadi, solusi akhir untuk paradoks Zeno adalah kura-kura menang pada kondisi A dan selanjutnya Achilles menang pada kondisi berbeda yaitu kondisi C.

Bagaimana dengan kondisi himpunan B?
Pertanyaan ini menarik dan lebih seru bila kita bahas dengan pendekatan deret dan limit tak hingga. Lagi pula Zeno masih penasaran, “Bagaimana caranya Achilles bisa menyalip kura-kura? Menyusul saja sulit!”
Spoiler for Solusi 3: dengan Deret dan Limit
Solusi Paradoks Zeno dengan Deret dan Limit.

Zeno telah meresahkan para ahli matematika sejak lebih dari dua ribu tahun yang lalu. Baru pada abad ke-19 ahli matematika dunia bernama Cauchi dapat menyelesaikan paradoks Zeno dengan sangat memuaskan. Cauchi menemukan solusi dengan limit deret tak hingga.



Penemuan deret tak hingga ini merupakan prestasi besar di bidang matematika. Bagaimana pun Zeno mendapat tempat terhormat karena telah mendorong berkembangnya teori limit deret tak hingga. Para ahli matematika mengkonfirmasi bahwa deret tak hingga ini benar-benar telah menyelesaikan paradoks dan memiliki penerapan luas di jaman sekarang â€" teknologi maju. Tetapi Zeno sendiri mengatakan,”Deret tak hingga tidak menyelesaikan paradoks,”

“Bagaimana bisa begitu?”

Ahli matematika kita, Cauchi, dengan cerdik langsung menghitung masalah yang diajukan Zeno. Berapa jauh sebenarnya yang ditempuh oleh kura-kura bila dilanjutkan sampai tak hingga langkah seperti penjelasan Zeno?

Dihitung dari titik Achilles mulai jalan maka jarak yang ditempuh oleh kura-kura adalah,

10 + 1 + 0,1 + 0,01 + 0,001 + … … … = S

Pada jaman Zeno, deret seperti di atas tidak bisa dihitung. Tetapi jaman sekarang kita dapat memanfaatkan aljabar dan notasi angka yang mudah.

Kalikan kedua ruas dengan 0,1 maka
0,1(10 + 1 + 0,1 + 0,01 + …. … .. ) = 0,1(S)
1 + 0,1 + 0,01 + 0,001 + … … … = 0,1(S)

Kurangkan persamaan terakhir ke persamaan awal kita peroleh,

10 = S â€" 0,1(S) = 0,9 S
Atau
S = 10/0,9 = 100/9 meter

Jadi, jarak yang ditempuh kura-kura ternyata tidak jauh-jauh amat. Hanya 100/9 meter = 11,111 meter. Tidak lebih dari 12 meter. Tentu saja kita menduga bahwa Achilles tidak akan kesulitan menempuh jarah seperti itu! Memang benar demikian.

Berapakah jarak yang ditempuh Achilles sesuai cerita Zeno?

K = 10 + 1 + 0,1 + 0,01 + 0,001 + … … …

Sekilas kita lihat jarak tempuh Achilles mirip dengan jarak tempuh kura-kura pada akhirnya. Dengan cara yang sama kita dapat menghitung jarak Achilles adalah,

K = 100/9 m

Karena jarak Achilles pada akhirnya sama dengan jarak yang ditempuh oleh kura-kura maka Achilles berhasil menyusul kura-kura.

S = K = 100/9 = 11,111 m

Setelah Achilles berhasil menyusul maka Achilles akan meninggalkan kura-kura di belakang dan Achilles memenangkan lomba balap itu.
Zeno keberatan, ”Tapi apakah Achilles memiliki waktu yang dibutuhkan untuk menyusul?” Zeno membayangkan bahwa Achilles akan membutuhkan waktu tak hingga.

Kita dengan mudah dapat menunjukkan bahwa waktu yang dibutuhkan juga cuma sebentar.
w = jarak / kecepatan
= (100/9)/10
= 10/9 = 1,111 detik.

Tidak lebih dari 2 detik Achilles sudah menyusul kura-kura. Bahkan lama waktu yang dibutuhkan juga dapat kita hitung dengan deret. 10 meter butuh 1 detik. 1 meter butuh 0,1 detik, dan seterusnya.

w = 1 + 0,1 + 0,01 + 0,001 + … … …

Kalikan kedua ruas dengan 0,1 maka kita peroleh,

0,1 w = 0,1 + 0,01 + 0,001 + … … …

Kurangkan yang terakhir dengan yang awal,

w â€" 0,1w = 1
0,9 w = 1
w = 1/0,9 = 10/9 = 1,111…

Hasilnya konsisten, hanya butuh waktu 1,111 detik Achilles akan menyusul kura-kura. Zeno berpikir sejenak. Penjelesan deret di atas tampaknya benar dan konsisten. Zeno masih mencari-cari lubang kesalahan dari penjelasan di atas. Dan Zeno memang menemukan lubang kelemahan deret di atas.

Cara lebih sederhana menjelaskan keberatan Zeno adalah dengan memakai pecahan desimal berulang. Dalam kasus kita, Zeno mengarahkan agar kita percaya bahwa,
10 + 1 + 0,1 + 0,01, + 0,001 + … … … = 11,111….
adalah bilangan tak hingga. Dengan mudah kitadapat menghitungnya.
Misal,
11,111… = x
Kalikan kedua ruas dengan 10,
111,111… = 10x
Kurangi yang akhir dengan yang pertama,
10x â€" x = 111,111… â€" 11,111 …
9x = 100
x = 100/910 (Sebuah bilangan pecahan biasa).

Dengan mudah kita dapat menyelesaikan masalah Zeno. Pada jamannya, Zeno dan ahli matematika lain tidak dapat melakukan perhitungan seperti di atas. Karena saat ini belum ditemukan teori aljabar dan notasi pecahan desimal. Jadi wajar saja, paradoks Zeno tak terselesaikan waktu.

Tetapi penemuan paling besar untuk menyelesaikan paradoks Zeno adalah teori limit tak hingga untuk deret geometri. Penemuan limit tak hingga ini menjadi dasar pengembangan ilmu dan teknologi ratusan tahun kemudian sampai sekarang. Inilah kehebatan matematika.

Jadi, paradoks Zeno telah terselesaikan. Matematika menjadi makin berkembang. Para ahli matematika dan masyarakat bergembira.



Sumber: apiqquantum

Sumber :http://www.kaskus.co.id/thread/5365cb306607e7b5098b4665